Es una coordenada bien definida. dada por una abscisa y una ordenada en el plano cartesiano, por ejemplo, el par ordenado ( 5, 2 ) quiere decir que la abscisa es 5 y es la distancia del eje x (eje de las abscisas) al eje y (eje de las ordenadas) y la ordenada es 2 e indica la distancia del eje y al eje x. Un par ordenado tiene la característica principal y fundamental de tener uno y sólo un valor para x y un único valor para y.
Ejemplo:
En el plano cartesiano se representa la pareja ordenada (5,2); que representa un punto o una coordenada cartesiana

DISTANCIA ENTRE
DOS PUNTOS EN EL PLANO CARTESIANO
Dados dos puntos cualesquiera A(x1, y1), B(x2, y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento
que los separa.
Cuando los puntos se encuentran ubicados sobre el eje x (de las abscisas) o en una recta
paralela a este eje, la distancia entre los puntos corresponde al valor
absoluto de la diferencia de sus abscisas (x2 – x1).
Cuando los puntos se encuentran ubicados sobre el eje y (de las ordenadas) o en una recta
paralela a este eje, la distancia entre los puntos corresponde al valor
absoluto de la diferencia de sus ordenadas.
Ahora, si los puntos se encuentran en cualquier lugar del
sistema de coordenadas, la distancia queda determinada por la relación:




Demostración
Sean P1 (x1, y1) y P2 (x2, y2) dos puntos en el plano.
La distancia entre los puntos P1 y P2, se denota por , y está dada por:
, y está dada por:
La distancia entre los puntos P1 y P2, se denota por
 , y está dada por:
, y está dada por:
En la Figura
1, se han localizado los puntos P1 (x1, y1) y P2 (x2, y2) así como también el segmento de
recta

Al trazar por el punto P1 una paralela al eje x (abscisas) y por P2 una paralela al eje y (ordenadas),
éstas se interceptan en el punto R,
determinando el triángulo rectángulo P1RP2 y en el cual podemos aplicar el Teorema de Pitágoras:
Pero:

y:

Luego,

En la fórmula (1) se observa que la distancia
entre dos puntos es siempre un valor positivo.
El orden en el cual se restan las coordenadas
de los puntos P1 y P2 no afecta el valor de la distancia.
PRODUCTO CARTESIANO
Sean dos conjuntos (A y B) no vacíos denominaremos producto cartesiano entre A y B al conjunto de todos los pares ordenados cuya primera componente pertenece al conjunto A y la segunda componente al conjunto B, simbólicamente se lo representa: A X B
Ejemplo:
Puedes alcanzar una mayor claridad visualizando el siguiente video:
RELACIÓN
Lo primero es entender que Correspondencia es equivalente a Relación. En nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”.
Ejemplos:
En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio.
En el directorio telefónico, cada persona está relacionada con un número; o sea, a cada nombre de la guía le corresponde un número.
Sean A y B dos conjuntos no vacíos y bien definidos. La relación es la correspondencia entre los elementos del primer conjunto (A), llamado Dominio, con los elementos del segundo conjunto (B), llamado Recorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
Ejemplos:
1. En una tienda
comercial, cada artículo está relacionado con su precio; o sea, a
cada artículo le corresponde un precio.
2. En el directorio telefónico, cada persona está relacionada
con un número; o sea, a cada nombre de la guía le corresponde un número.
Se define como: R ⊆ AXB
Diagrama sagital
Es aquel gráfico que se utiliza para representar funciones y
relaciones.
Ejemplos:
Ejemplos:
1. 
 Diagrama Cartesiano
Diagrama Cartesiano

 Diagrama Cartesiano
Diagrama Cartesiano
2. 



DOMINIO Y RANGO DE UNA RELACIÓN
El dominio de una relación es el conjunto de preimágenes; es decir, el conjunto formado por los elementos del conjunto de partida que están relacionados con elementos del conjunto de llegada. Al conjunto de imágenes, esto es, elementos del conjunto de llegada que están relacionados, se le denomina recorrido o rango.
Para el primer ejemplo, el dominio (Dom) de la relación R corresponde a:
Dom = { 1,2,3,4}
Y el rango (Ran) está definido como:
Ran = { 3,5,7,9 }
Para el segundo ejemplo:
Dom = {1,3,4,5} ;
Ran = {1,3,5,7,9,10}
Visualiza el siguiente video para profundizar en el tema
Clases de Relación
1. Relación
inyectiva
Una relación o correspondencia es inyectiva cuando cada uno
de los elementos del conjunto de llegada es como máximo imagen de uno de los
elementos del conjunto de partida, o bien, no es imagen de ningún elemento.
2. Relación Sobreyectiva o Suprayectiva
Cuando todos y cada uno de los elementos del conjunto de
llegada es imagen de por lo menos un elemento del conjunto de partida.


3. Relación Biyectiva
Una relación es biyectiva cuando es inyectiva y
sobreyectiva, es decir, que a cada elemento del conjunto de partida le
corresponde uno y sólo un elemento del conjunto de llegada y cada elemento del
conjunto de llegada es imagen de un solo elemento del dominio


APLICACIONES O FUNCIONES
Sean A y B dos conjuntos no vacíos y bien definidos. Una relación de A en B en la que a todo elemento de A le corresponde un único elemento de B, se le llama función.
La simbolización de las funciones se hace comúnmente mediante las letras minúsculas f, g o h, o cualquiera de las demás.
Se escribe:
Veamos un ejemplo:Se escribe:
Las relaciones inyectivas, sobreyectivas y biyectivas son
relaciones funcionales, es decir, son relaciones y además, funciones.
Por lo
anterior podemos decir que toda función es una relación pero no toda relación
es una función.
Los siguientes conjuntos representan algunos de los equipos del fútbol profesional colombiano y las respectivas ciudades donde juegan de locales
A = { Medellín, Ibagué, Bogotá, Cali }B = { Nacional, Deportivo Cali, Deportes Tolima, Millonarios}
La función f(x), mediante parejas ordenadas sería:
f(x) = { (Medellín, Nacional), (Ibagué, Deportes Tolima),
(Bogotá, Millonarios), (Cali, Deportivo Cali) }
Mediante un diagrama sagital, la representación sería la siguiente:

Se puede reforzar el concepto en el siguiente video
Gráfica de una Función
Retomando el
concepto de función lineal que fue visto en el grado 9º, analicemos la función:
f(x) = x + 2, que es una función

Procedemos a darle valores a x, para elaborar la siguiente tabla y de acuerdo a ella, la respectiva gráfica:
Hacemos, y = f(x)
f(-6) = - 6 + 2 = - 4
f(-4) = - 4 + 2 = - 2
f(1) = 1 + 2 = 3
f(2) = 2 + 2 = 4
f(3) = 3 + 2 = 5
Hacemos, y = f(x)
f(-6) = - 6 + 2 = - 4
f(-4) = - 4 + 2 = - 2
f(1) = 1 + 2 = 3
f(2) = 2 + 2 = 4
f(3) = 3 + 2 = 5

La función
f(x) = x + 2; es
· Inyectiva porque cada uno de los elementos del
conjunto de llegada o rango es imagen de un único elemento de X
· Sobreyectiva porque cada uno de los elementos
del eje Y pertenecen al rango
· Biyectiva ya que es Inyectiva y sobreyectiva
Dominio y Rango de una Función
En una función el dominio está dado por todos los elementos
del eje X que tienen imagen en el eje Y
El rango de
una función está dado por aquellos elementos del eje Y que son imagen de algún
elemento del eje X
Para el caso de la función f(x) = x + 2, su dominio y rango corresponde a los Números Reales (R).
Para el caso de la función f(x) = x + 2, su dominio y rango corresponde a los Números Reales (R).
Variable independiente y variable
dependiente
En el eje X se representa la variable independiente, que es
aquella cuyo valor no depende del que tome otra variable. Ejemplos: dolor de
cabeza con respecto a la aspirina, masa muscular y ejercicio con pesas, el
tiempo con respecto a un espacio recorrido.
Variable
dependiente es aquella cuyo valor depende del que tome otra variable
La gráfica de una función se interpreta de izquierda a
derecha y de abajo hacia arriba.
Función creciente
Una función
es creciente cuando a medida que aumenta su valor en X, también aumenta en Y.




Función Decreciente
Una función es decreciente cuando a medida que aumenta su valor en X, el valor de Y disminuye
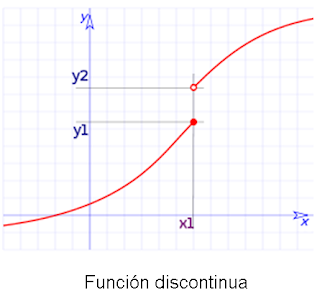
Funciónes continuas y discontinuas
Una función
es continua cuando para dibujar su gráfica, no es necesario levantar el lápiz.
Todos los elementos del eje X pertenecen al dominio. En el caso contrario, la
función es discontinua

FUNCIÓN PERIÓDICA
Las funciones periódicas son funciones que se comportan en una manera cíclica (repetitiva) sobre un intervalo especificado (llamado un periodo). La gráfica se repite a si misma una y otra vez así como es trazada de izquierda a derecha. En otras palabras, la gráfica completa puede ser formada de copias de una porción particular, repetida en intervalos regulares indefinidamente. Si f es conocida sobre un periodo entonces es conocida en todas partes.
Más formalmente, una función f es periódica si existe un número real P tal que f(x + P) = f(x) para todas las x.
Ejemplo:En este caso, el periodo es 2π
FUNCIÓN TRIGONOMÉTRICA
Una función trigonométrica f es aquella que está asociada a una razón trigonométrica. Éstas extienden su dominio a los números reales.
Su abreviatura son sen o sin (del latín sinus).
La gráfica de la función seno es:
La gráfica de la función seno es:
Codominio: [-1,1]
Continua: en X
; Periódica: si 2 π
COSENO
El coseno de un ángulo α se define como la razón entre el cateto contiguo (b) y la hipotenusa (c).



Codominio: [-1,1]
El coseno de un ángulo α se define como la razón entre el cateto contiguo (b) y la hipotenusa (c).
Su abreviatura es cos (del latín cosinus).
La gráfica de la función coseno es:
La función del coseno es periódica de período 360º (2π radianes).
Dominio: RCodominio: [-1,1]
Continua: en X
; Periódica: si 2 π
TANGENTE
La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo (b).


La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo (b).
Su abreviatura son tan o tg.
La gráfica de la función tangente es:
Discontinua : en X ; Periódica: si cada π
Continua: en Y
Continua: en Y
Su abreviatura es cot, cotg o cotan.
La gráfica de la función cotangente es:
La función de la cotangente es periódica de período 180º (π radianes).
Dominio: (0, π) U (π, 2 π) Codominio: R
SECANTE
La secante es la razón trigonométrica inversa del coseno, es decir sec α · cos α=1.
La secante de un ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto contiguo (b)


Su abreviatura es sec.
La gráfica de la función secante es:

La función de la secante es periódica de período 360º (2π radianes).
Dominio: [0, π/2) U ( π/2, 3π/2) U ( 3π/2, 2 π]
Codominio: R - (-1,1)
COSECANTE
La cosecante es la razón trigonométrica inversa del seno, es decir csc α · sen α=1.
La cosecante del ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).
Su abreviatura es csc o cosec.
La gráfica de la función cosecante es:
La función de la cosecante es periódica de período 360º (2π radianes).
Dominio: (0, π) U (π, 2π)Codominio: R - (-1,1)
Material sobre funciones trigonométricas tomado de
ÁNGULO GENERADO
En un sistema de coordenadas rectangulares se dice que un ángulo está en posición estándar o normal si su vértice está en el origen y el lado inicial está en el eje positivo x. El ángulo se menciona con frecuencia en términos del cuadrante en el cual está el lado terminal.
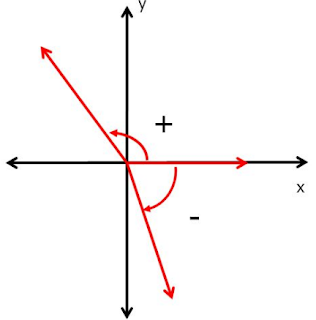
ÁNGULOS POSITIVOS Y NEGATIVOS
Para formar un ángulo q se comienza con un lado denominado lado inicial en una posición fija. Después se comienza con el segundo lado, denominado lado terminal en la misma posición que el lado inicial y se rota el lado terminal en un plano alrededor de 0 hasta encontrar la posición final. Una rotación en sentido contrario a las manecillas del reloj produce un ángulo positivo; una rotación en el sentido de las manecillas del reloj, un ángulo negativo.

SIGNOS DE LAS FUNCIONES TRIGONOMÉTRICAS DE ACUERDO AL CUADRANTE
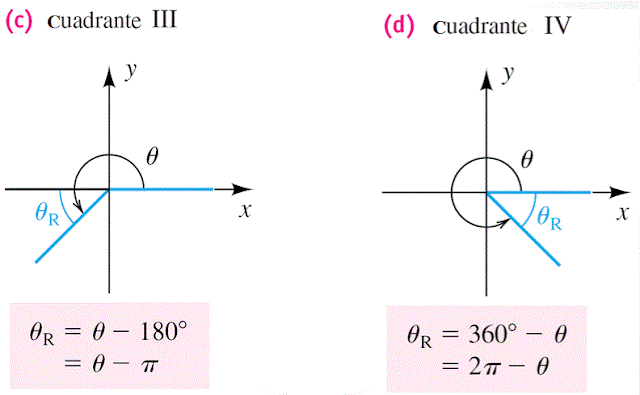
ÁNGULOS DE REFERENCIA
Sea θ un ángulo en posición estándar. El ángulo de referencia para θ es el ángulo agudo, θR , que el lado terminal de θ hace con el eje x

Algunos ejemplos de aplicaciones en el siguiente video





No hay comentarios:
Publicar un comentario