Esta ley se usa en aquellos ejercicios en los que se conocen los tres lados del triángulo y es preciso calcular uno o dos ángulos o cuando se conocen dos lados y el ángulo comprendido entre ellos y es necesario averiguar la medida del lado restante.
Observemos la demostración del teorema haciendo clic sobre la siguiente imagen
Ejemplos:
Observemos la demostración del teorema haciendo clic sobre la siguiente imagen
Ejemplos:
1. Desde lo alto de un globo se observa un pueblo A con un ángulo de 50º, y otro B, situado al otro
lado y en línea recta, con un ángulo de 60º. Sabiendo que el globo se encuentra a una distancia de
6 kilómetros del pueblo A y a 4 del pueblo B, calcula la distancia entre los pueblos A y B.
Solución:
Un esquema de la situación descrita, sería el siguiente:

El ángulo debajo del globo es de 110º porque si trazáramos una perpendicular desde el globo al
suelo, a la izquierda tendríamos 50º y a la derecha 60º. Aquí tendremos que usar el teorema del coseno, porque el ángulo que conocemos es el que forman
los dos lados de los cuales tenemos su longitud.

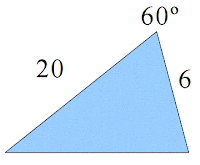
2. Una valla cuyo perímetro tiene forma triangular mide 20 metros en su lado mayor, 6 metros en
otro y 60º en el ángulo que forman entre ambos. Calcula cuánto mide el perímetro de la valla.
Solución:
La situación se puede entender de la siguiente forma
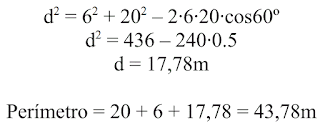
Tomado de:
Te invito a observar los siguientes videos para reforzar este concepto
Ejercicios Propuestos
1. Un automóvil viaja por una carretera en dirección Este, en línea recta, durante 1 hora; luego viaja en línea recta durante 30 minutos por otra
carretera que se dirige al Noreste y que en su origen forma un ángulo de 135º con la primera vía. Si el automóvil se desplaza a una velocidad constante de 40 km/hora, ¿qué tan lejos está de su posición de partida al terminar el recorrido?. Apóyate en el siguiente gráfico
2. Los lados de un triángulo son a = 20, b = 25, c = 22. Encontrar los ángulos del triángulo.

orales que buena onda amigo
ResponderEliminara. Una valla forma un ángulo de 80° con el piso y está sostenida por una viga de 15 metros de longitud.
ResponderEliminarLa viga va desde el borde de la valla hasta el piso formando un ángulo de 53° con éste. Calcular la
distancia que hay entre la base de la valla y la base de la viga. ayudaaaaaaaa
2): un lote de forma triangular esta bordeado por dos carreteras que se encuentran en un angulo de 80° los lados del lote miden 90 m y 80 m ¿cuantos metros mide el perimetro del lote? Diganme la sustentacion
ResponderEliminar