La ley de los senos es la relación entre los lados y ángulos de triángulos no rectángulos (oblicuos). Establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado.
El ∆ABC es un triángulo oblicuo con lados a, b y c, entonces 
Para usar la ley de los senos es necesario conocer ya sea dos ángulos y un lado del triángulo (AAL o ALA) o dos lados y un ángulo opuesto de uno de ellos (LLA).
Ejemplos:
En el punto A se encuentra un avión que viaja hacia el este, desde ahí a 70◦ grados hacia el
norte (izquerda del frente del avión) se encuentra un aeropuerto. Si avanza 100 kilómetros,
ubicándose el avión ahora en el punto B, el mismo aeropuerto está a 70◦ al sur respecto del
mismo avión. ¿A qué distancia se encuentran los puntos A y B del aeropuerto?
Solución

α = 70◦
, y β = 30º .
El tercer ángulo γ = 80º , porque 70º + 30º + 80º = 180º
Para calcular las distancias que queremos conocer aplicamos la ley de senos:

La distancia desde el punto A hasta el punto C es:

Reforcemos este concepto en los siguientes videos
Ejercicios Propuestos
1. halla la longitud del faro inclinado si se sabe que en el triángulo ABC que se observa el lado “b” mide 9,9
m, los ángulos A, B miden 42° y 53° respectivamente. Utiliza la siguiente gráfica

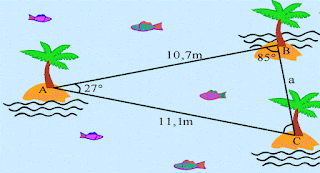
2. De acuerdo con el siguiente gráfico, calcula la distancia entre las palmeras B y C.
No hay comentarios:
Publicar un comentario